Рассмотрим диаграмму растяжения, которая показывает зависимость между растягивающей силой P, действующей на образец, и вызываемой ею деформацией Δl (рис. 1)

На диаграмме можно указать пять характерных точек:

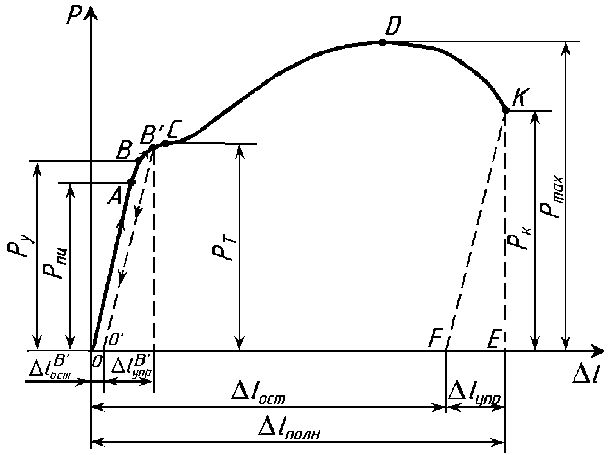
Рис.1 Диаграмма растяжения малоуглеродистой стали

Прямолинейный участок диаграммы ОА указывает на пропорциональность между нагрузкой Р и удлинением Δl. (Эта пропорциональность впервые была замечена в 1670 г. Робертом Гуком и получила в дальнейшем название закона Гука).

Величина силы Р_пц (точка А), до которой остается справедливым закон Гука, зависит от размеров образца и физических свойств материала.

Если испытуемый образец нагрузить растягивающей силой, не превышающей величину ординаты точки B (силы P_y ), а потом разгрузить, то при разгрузке деформации образца будут уменьшаться по тому же закону, по которому они увеличивались при нагружении. Следовательно, в этом случае в образце возникают только упругие деформации.

В случае, если растягивающее усилие выше P_y, при разгрузке образца деформации полностью не исчезают и на диаграмме линия разгрузки будет представлять собой прямую B'О', уже не совпадающую с линией нагружения, а параллельную ей. В этом случае деформация образца состоит из упругой Δl_упр^B' и остаточной (пластической) Δl_ост^B' деформации.

Таким образом, характерной особенностью точки B является то, что при превышении нагрузки P_y образец испытывает остаточные деформации при разгружении.

Выше точки В диаграмма растяжения значительно отходит от прямой (деформация начинает расти быстрее нагрузки, и диаграмма имеет криволинейный вид), а при нагрузке, соответствующей Р_т (точка С), переходит в горизонтальный участок. В этой стадии испытания в материале образца по всему его объему распространяются пластические деформации. Образец получает значительное остаточное удлинение практически без увеличения нагрузки.

Свойство материала деформироваться при практически постоянной нагрузке называется текучестью. Участок диаграммы растяжения, параллельный оси абсцисс, называется площадкой текучести.

В процессе текучести на отшлифованной поверхности образца можно наблюдать появление линий (полос скольжения), наклоненных примерно под углом 45° к оси образца (рис. 2а). Эти линии являются следами взаимных сдвигов кристаллов, вызванных касательными напряжениями.

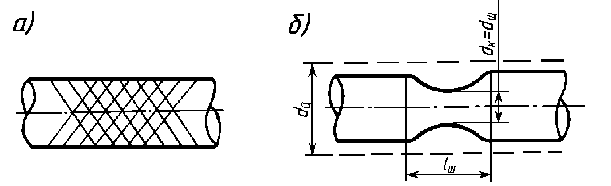
Рис.2 Образование линий сдвига (а) и местного сужения—шейки (б)

Линии сдвига называются линиями Чернова по имени знаменитого русского металлурга Д. К. Чернова (1839 - 1921), впервые обнаружившего их.

Удлинившись на некоторую величину при постоянном значении силы, т.е. претерпев состояние текучести, материал снова приобретает способность сопротивляться растяжению (упрочняться), и диаграмма поднимается вверх, хотя гораздо более полого, чем раньше. В точке D усилие достигает максимального значения P_max.

Наличие участка упрочнения (от конца площадки текучести до наивысшей точки диаграммы растяжения) объясняется микроструктурными изменениями материала: когда нагрузка на образец возрастает, микроскопические дефекты (линейные и точечные) группируются так, что развитие сдвигов кристаллов, вызванных касательными напряжениями, затрудняется, а потому сопротивление материала сдвигу начинает возрастать и приближаться к его сопротивлению отрыву.

При достижении усилия P_max на образце появляется резкое местное сужение, так называемая шейка (рис. 2б), быстрое уменьшение площади сечения которой вызывает падение нагрузки, и в момент, соответствующий точке К диаграммы, происходит разрыв образца по наименьшему сечению шейки.

До точки D диаграммы, соответствующей P_max, каждая единица длины образца удлинилась примерно одинаково; точно так же во всех сечениях одинаково уменьшались поперечные размеры образца. С момента образования шейки вся деформация образца локализуется на малой длине (l_ш~ 2d₀) в области шейки, а остальная часть образца практически не деформируется.

Абсциссы диаграммы растягивания OE, OF и FE, характеризующие способность образца деформироваться до наступления разрушения, соответствуют полному абсолютному удлинению образца Δl_полн, остаточному абсолютному удлинению Δl_ост и абсолютному упругому удлинению образца Δl_упр.

Для определения упругой деформации в момент разрыва необходимо из точки K диаграммы провести прямую KF, параллельную прямолинейному участку OA, так как упругие деформации при разрыве также подчиняются закону Гука.

Хрупкие материалы, типичным представителем которых является чугун, дают диаграмму растяжения иного характера (рис. 3).

Рис.3 Диаграмма растяжения чугуна

Чугун разрушается внезапно при весьма малых деформациях, составляющих порядка (0,5-0,6)% от расчетной длины образца l₀, и без образования шейки. Диаграмма при этом не имеет явно выраженного прямолинейного участка (отклонение от закона Гука начинается очень рано), площадки текучести и зоны упрочнения.

При испытании на растяжение хрупких материалов определяют, как правило, только максимальную нагрузку P_max.

Обычно при практических расчетах для хрупких материалов отклонение от закона Гука не учитывают, т. е. криволинейную диаграмму заменяют условной прямолинейной диаграммой.